Permasalahan rekursif yang sering dibahas adalah deret Fibonacci. Deret Fibonacci adalah deret bilangan yang nilainya di ambil dari hasil penjumlahan 2 angka sebelumnya. Perhatikan deret Fibonacci berikut:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Deret Fibonacci ke 0 adalah 0, deret Fibonacci ke 1 adalah 1, deret Fibonacci ke 2 adalah 1, deret Fibonacci ke 6 adalah 8, dan seterusnya.

Rumus Deret Fibonacci?

Deret Fibonacci memiliki rumus sebagai berikut:

Rumus tersebut dapat kita baca:

Jika n besar dari 1, maka Fibonacci ke n adalah penjumlahan antara Fibonacci ke n-1 dan Fibonacci ke n-2. Sedangkan jika n = 1 atau n = 0, maka Fibonacci ke n adalah n itu sendiri.

Dari rumus di atas terlihat jelas bahwa rumus Fibonacci di atas adalah rumus rekursif. Karena di dalam rumus tersebut ada pemanggilan rumus Fibonacci itu sendiri, yaitu pada F(n-1)+F(n-2). Pemanggilan rumus tersebutlah yang akhirnya disebut sebagai rekursif.

Kita dapat implementasi langsung rumus Fibonacci tersebut ke dalam kode program Java seperti berikut ini:

Penjelasan Rumus Fibonacci

Perhatikan kembali rumus Fibonacci berikut ini:

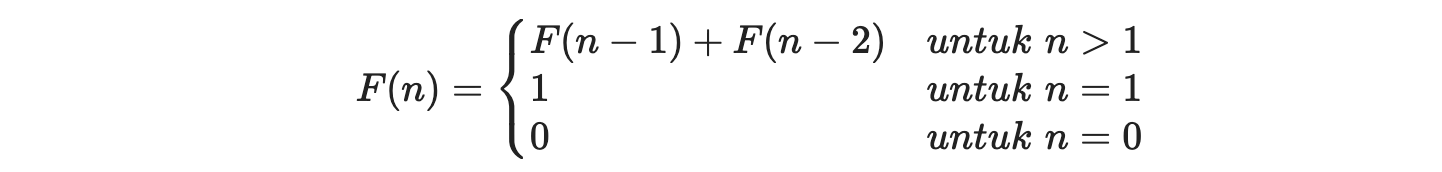
Rumus di atas memiliki 3 kondisi. Setiap kondisi akan menghasilkan perhitungan yang berbeda. Berikut cara perhitungannya:

1. Jika n lebih besar dari 1, maka F(n) = F(n-1)+F(n-2)
2. Jika n sama dengan 1, maka F(1) = 1
3. Jika n sama dengan 0, maka F(0) = 0

Ketiga kondisi persis sama dengan yang kita buat pada kode programnya, perhatikan potongan kode program berikut:

Mengapa Menggunakan return

Keyword return pada java menyebabkan sebuah fungsi atau method menghasilkan nilai. Nilai yang dihasilkan ini sangat penting pada rumus Fibonacci, karena nilai yang dihasilkan tersebut akan dijumlahkan dengan nilai yang dihasilkan oleh rumus itu juga. Perhatikan baris kode program berikut:

Rumus F(n-1) harus menghasilkan nilai, agar dapat dijumlahkan dengan rumus berikutnya yaitu F(n-2).

Selanjutnya

Deret Fibonacci sangat cocok digunakan untuk membahas dan memahami tentang konsep Rekursif. Namun, masih ada beberapa contoh kasus lain yang dapat digunakan untuk memperdalam pemahaman tentang Rekursif, di antaranya:

1. Tower of Hanoi
2. Permutasi
3. Faktor Persekutuan Terbesar (FPB)
4. Binary Search